首页
登录
注册
-
氢气作为一种清洁能源，经过燃烧或电化学反应可产生净零排放的能量；另一方面，它用于金属氧化物矿石的还原，相比传统的基于碳还原的冶金工艺，相应产物仅为水，避免了大量的环境污染及碳排放。等离子体是在一定电磁场激励下部分气体分子被激发、电离或离解而产生的具有相应反应活性的混合物，其中低温等离子体又称非平衡等离子体，应用于氢气可以产生还原性更强的氢等离子体，用于炼铁时可在相对低温条件下实现实现固态氧化铁的直接还原[1]。氢气还原炼铁将为传统碳排放和污染大户的炼铁行业带来绿色革命，而等离子体辅助氢气还原预期将明显改善这一工艺的实现条件及能耗。具体来说，由于激发态物质携带的能量可以有效地在还原反应界面释放[2]，其不需要体加热，整体温度较低，减少了来自于反应器的热损耗，预期将有效降低工艺能耗，节约成本。
等离子体有不同的产生方式，其中微波等离子体因其无极放电、放电区域集中，放电稳定，放电均匀性较好[3,4]等特征在表面镀膜、刻蚀[5-9]等领域有广泛应用。在还原氧化铁方面，该类等离子体也已经有一定研究[1,10-12]，Sabat[13]在研究中指出氢气等离子体相比焦碳热还原需要更少的能量。Rajput[14]在实验中使用微波谐振腔式等离子体探究了不同操作参数下氢气等离子体对氧化铁的还原能力，得出了微波功率密度、氢气流速、气体压力、温度等因素对还原效果有重要影响。徐慢[15]在氢气、甲烷微波等离子体环境下对钛铁矿进行还原，发现微波功率的提高有助于钛铁矿的还原。微波等离子体的发生包括电子回旋共振（ECR）、表面波和谐振腔三种方式，谐振腔式又包括石英管式、圆柱谐振腔等结构类型，其中石英管式结构较简单，可拓展性较强，文献[16]针对其反应结构进行优化，以实现多微波源在反应器内的电场叠加增强。目前的研究多是从宏观实验的角度探索微波功率等对于低温等离子体还原氧化铁的影响，对于微观反应过程以及反应机理尚不够清楚。鉴于此，本文拟基于数值方法并结合相关文献实验结果，研究氢气在微波激发下的等离子体反应特性，进一步探究微波氢气放电等离子体与氧化铁还原相关的特征机理。
-
等离子体机理模型包括一系列物理化学方程，其中最重要的是电子输运方程、电子能量输运方程以及重物质输运方程。由于石英管式微波等离子体产生机制是通过波导输入的高强电磁场激发工质气体，其中电子起传输能量的关键作用，电子输运和电子能量输运方程如下
其中ne和nε分别表示电子密度和电子能量密度，Гe和Гε分别表示电子和电子能量的通量，通量由两部分组成，分别是迁移量和扩散量。Re和Rε表示化学反应引起的电子生成或者消耗，方程右边最后一项表示对流项，由于本文研究暂时不关注介质对流特性及影响，因此根据文献数据取一恒定对流速度u。
在低温氢等离子体中，重物质包括氢气分子（H2），激发态氢气分子（如H2s），离子态氢（H2+、H+、H3+）、原子氢（H）、激发态氢原子（Hs）等。据研究，在低温条件下66%的输入能量被用以生成振动激发态氢分子[17]，其被认为对氧化铁的还原起决定性作用[2,14,18]。因此本研究将这一活化分子作为主要研究对象，基于低温等离子体的低电离率的特性，构建相关化学反应，其主要包括电子碰撞反应、体反应和表面反应。其中电子碰撞反应是是整个反应体系的核心，对于低温等离子体，本研究主要采用了如表1所示的电子碰撞反应。
表1中反应R1~R6所对应碰撞截面参数来自LXcat数据库；电子碰撞反应速率常数可通过对电子能量积分得到：
式中ε表示电子能量，f(ε)表示电子能量分布函数（EEDF），其服从麦克斯韦分布，σ(ε)表示电子碰撞反应的碰撞截面参数，γ定义为
式中q为电子电荷，me为电子质量。
重物质模型中包括体反应和表面反应，主要化学反应如表2所示。
表2中R12-R16为表面反应，为壁面等离子体反应，其反应特性将在下文重物质输运边界条件讨论。重物质输运模型基于等离子体混合物对流扩散模型，服从Maxwell-Stefan方程：
式中ρ表示混合物密度，Wk表示物质质量分数，Rk表示反应源/汇项，jk为物质质量通量，由输运模型决定。
-
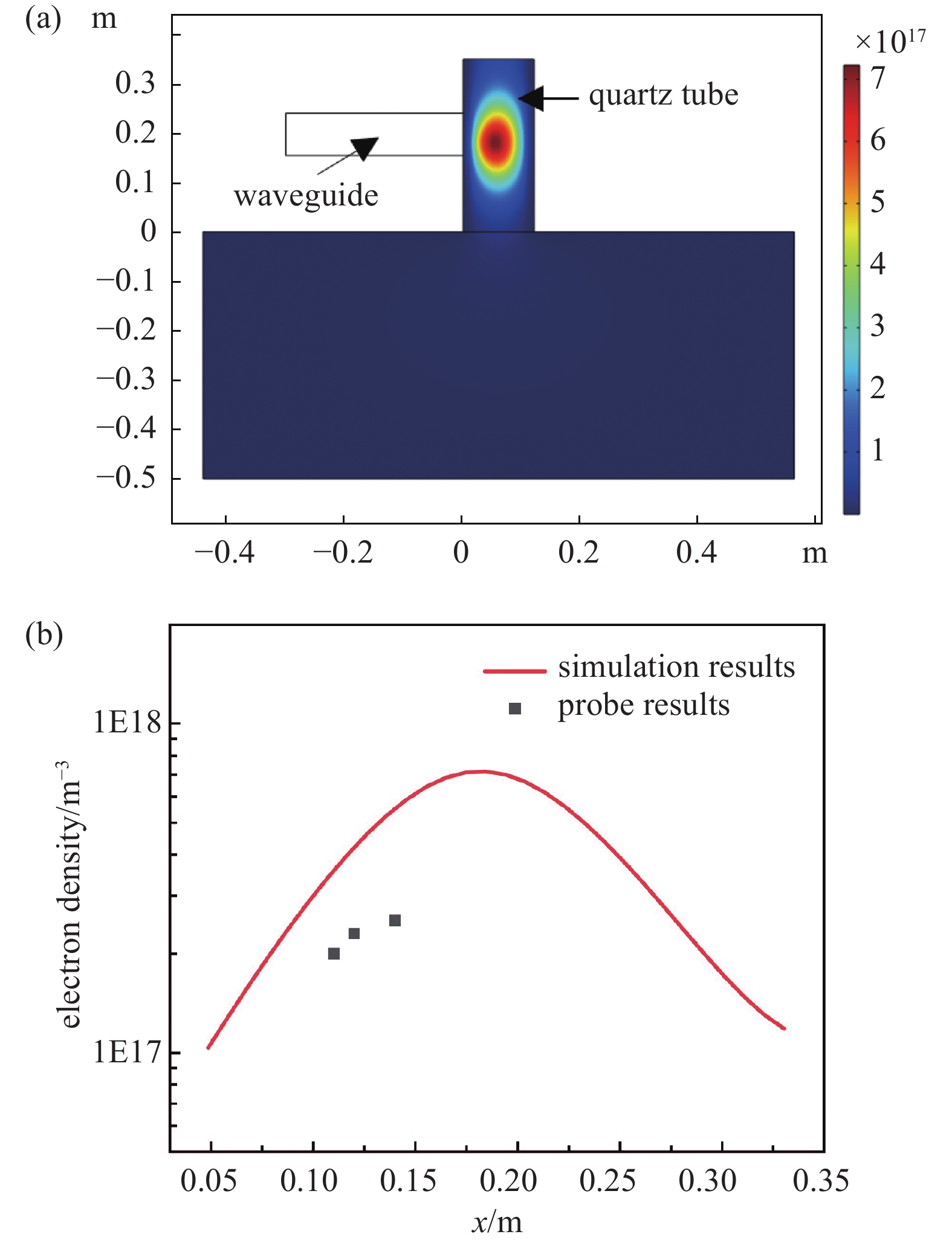
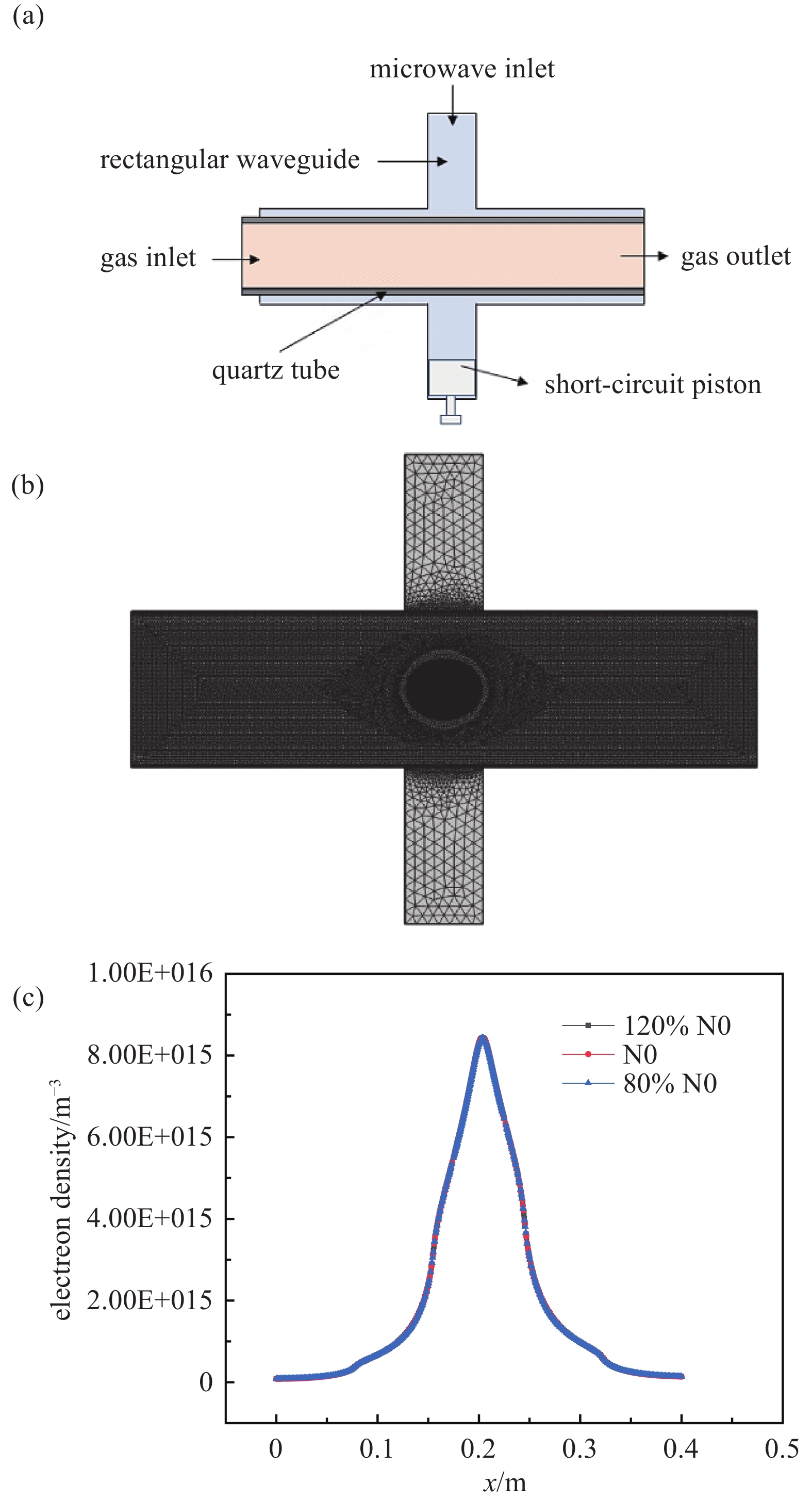
本文选择的石英管式微波谐振腔等离子体发生器，其主要由短路活塞以及石英管构成[22]，基于此反应器，基于有限元方法构建了相应二维等离子体反应模型，如图1所示。
图1(a)为二维简化微波等离子体反应器模型设置，其中石英管长0.4 m，宽0.1 m，微波波导宽0.05 m。微波从纵向波导上方端口入射，气体在横向石英管内流动，微波激励等离子体在石英管内产生。本文除等离子体模型验证部分，均采用此等离子体反应器结构。其中微波导及石英管在交汇处之外的侧壁均设为理想电导体边界，没有微波溢出，本文所研究各等离子体工况依条件参数不同整体微波路径损耗均在0.1%附近，压力及功率参数越大损耗相对越大。等离子体存在于横管流体区域，其网格须足够细化，并设置流动边界层，如图1(b)所示。模型进行了网格无关性检验，基于图1(a)所示装置，在微波功率为600 W，氢气压力为1400 Pa，流速为0.4175 m/s工况下，分别采用不同数目三套自由三角形网格进行计算，所确定网格数目N0为67594，另外两套分别为在此基础上粗化至80%和细化至120%，取某一反应时刻横向石英管轴线上电子密度分布如图1(c)所示，证明网格足够精确。
-
模型边界条件包括静电边界条件、电子输运边界条件和重物质输运边界条件。考虑到实际工况，静电条件设置为壁面处接地，其中电子输运边界条件为简化模型，不计热运动下电子在壁面的反弹，考虑壁面在一定电子轰击条件下的二次电子发射，即式(1)中的Гe和Гε在壁面处包含了二次电子发射通量。重物质输运的边界条件体现在表面的等离子体化学反应，即表2中的表面反应部分，对于等离子体表面反应的气相物质采用其黏附系数表征反应速率，模型中都设置为1。为初步探索微波氢气等离子体的反应特性，等离子体模块中气体介质按理想气体处理，取模型温度为常温300 K，对流项速度为0.4175 m/s，初始电子能量ε0为4 eV；模型取常用微波频率2.45 GHz，电磁波模式为TE模式。
-
本文首先基于Ar气氛微波等离子体研究初步检验模型的正确与可靠性，采用文献[23]中石英管式单波导微波装置及相应条件设置，Ar气体压力0.1 torr，温度300 K，输入300 W频率2.45 GHz的微波，结合前述等离子体模型进行模拟，与文献[23]中实验结果进行对比，所得电子密度分布及对比如图2所示。
须指出，由于等离子体反应测量的困难性等因素，通常认为数值模拟与实验结果在数量级上一致即可证明模型有效性[24]。实验中测量位置分别在其波导下方2 cm、4 cm、5 cm处，其结果与本文模拟结果对比如图2(b)所示，给出了沿管轴向的电子密度分布，两者数量级均为1017，可初步证明本文等离子体模型的合理性。
另外在上述Ar等离子体验证的基础上，针对本文石英管谐振腔氢气放电体系，选用文献[25]中4.5、9和30 W/cm3的微波功率密度(MWPD)，1400、2500和11000 Pa的压力进行模拟。不同工况所得电子密度量级分布在1016 ~1017 /m3之间，而文献在相同输入参数下计算出氢气等离子体电子密度的范围是不大于1017 /m3，与本文结果相符，进一步验证本文等离子体体系模型的合理性。
-
在微波等离子体产生过程中，微波入射功率起关键作用，氢气激发形成低温等离子体所需要的能量都来自于微波谐振腔内形成的电磁场。另外，所产生等离子体参数与其介质的压力密切相关。基于图1的等离子体装置，取氢气流速为0.4175 m/s，压力1400 Pa，根据理想气体状态方程：
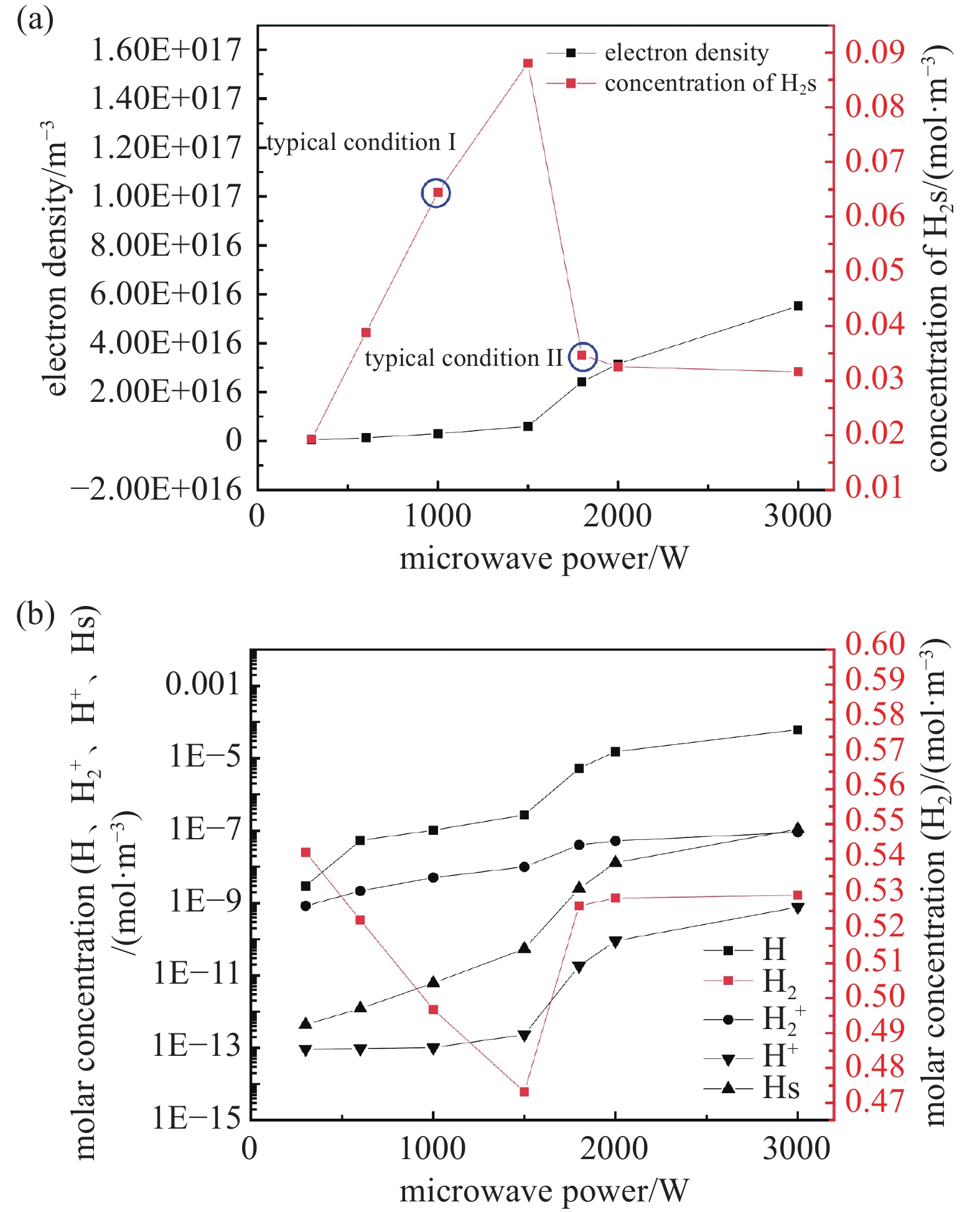
其中p为气体压力，V为气体体积，n为气体的物质的量，Rg为摩尔气体常数，T为温度，可得初始氢气浓度为0.56 mol/m3，模型温度300 K。选取微波功率分别为300 W、600 W、1000 W、1500 W、1800 W、2000 W和3000 W，取等离子体反应稳定时的结果进行分析。除主体指标电子密度和H2s外，作为对比同时给出了所形成等离子体中其它粒子成分相应变化特性，并与前两者进行对比，以更好地揭示低温条件下氢气等离子体特性，见图3。
由图3(a)可以看出，在其它条件不变的情况下，电子密度随微波功率升高而升高，在超过1500 W后产生的电子密度加速上升，同时产生的H2s的浓度呈快速下降。同时，在图3(b)中可以看出H2浓度与3(a)中H2s浓度随功率存在强反向相关变化趋势，也说明了H2s是该等离子体反应的主要产物，相应地，随着大量的H2分子被激发为H2s，其浓度快速减小，并在1500 W时达到极小值，同时H2s浓度达到峰值0.088 mol/m3。即随着功率超过~1500 W，H2s大部分退激发恢复为基态H2分子，这样前者快速降低而后者快速升高。另外随着功率升高，少部分其它活性粒子生成，其趋势与电子密度相似，其中H原子浓度相对最大，H+相对最少。
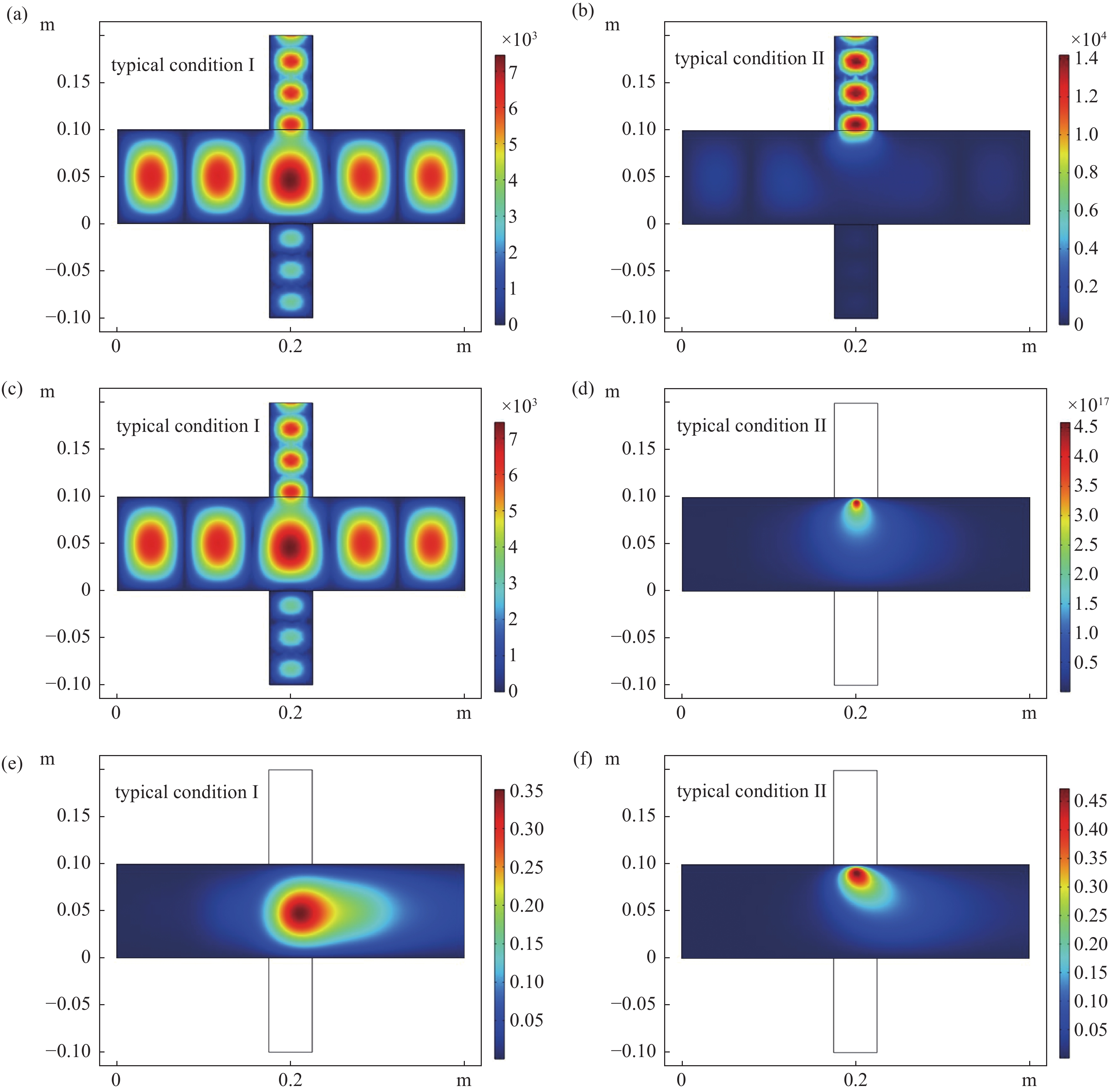
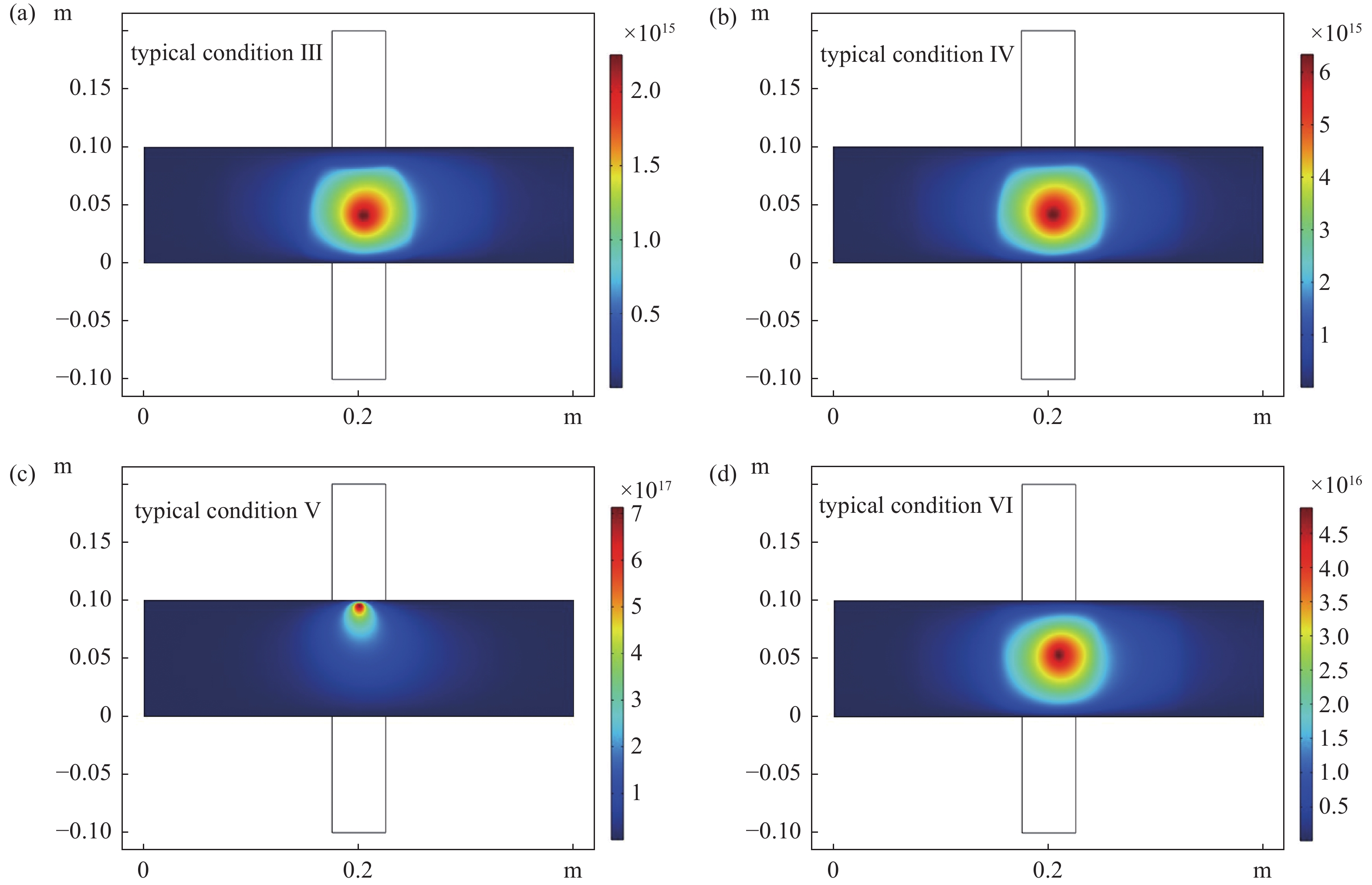
为进一步揭示该等离子体反应相关机理，选取图3中两个典型工况，其功率分别为1000 W和1800 W，对比分析反应器石英管内特征参数电场、电子密度和H2s摩尔浓度的分布，如图4所示。
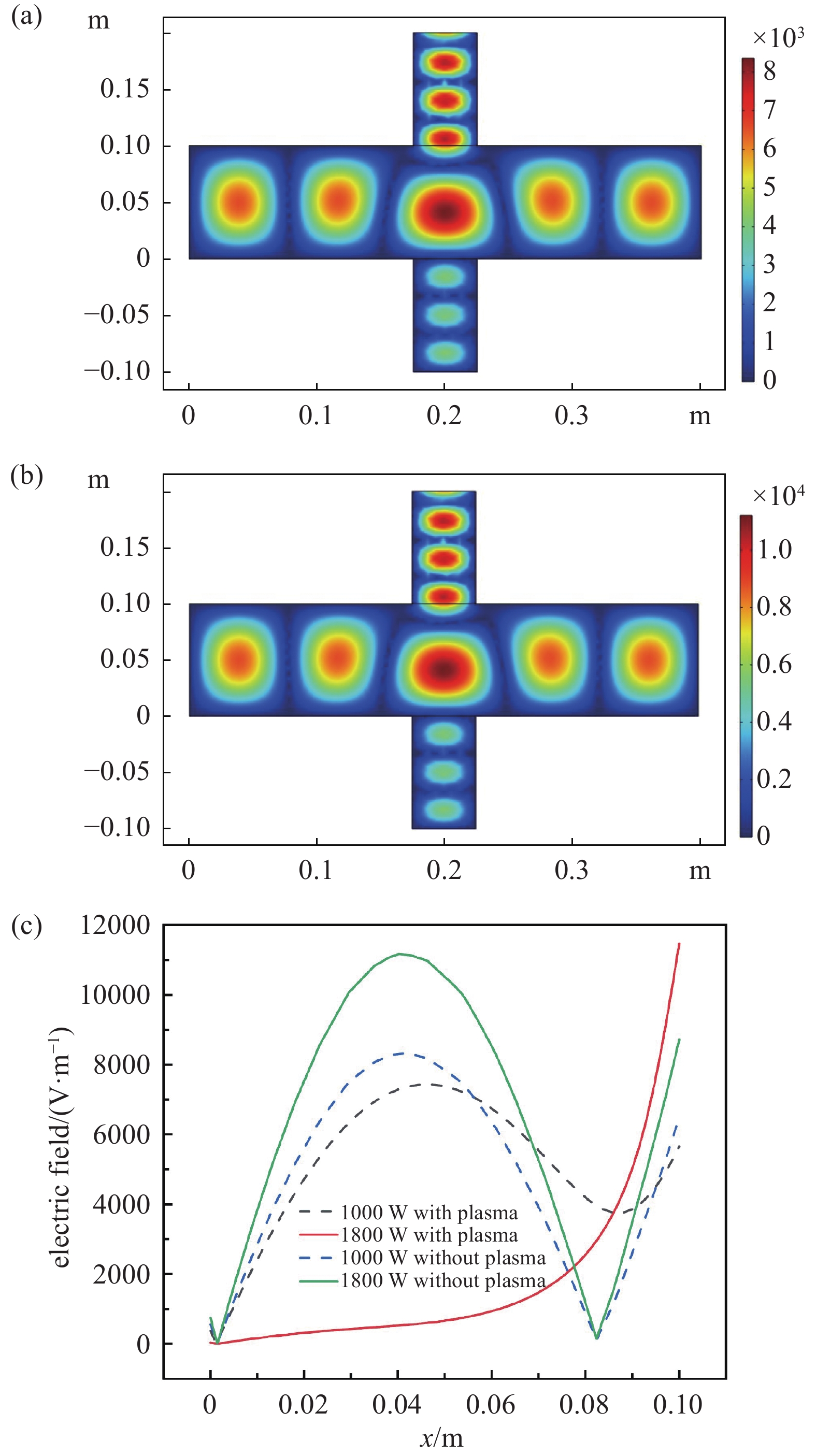
图4可以看出，功率适当时，所产生的等离子场规则分布在石英管内，如图4(a)(c)(e)；当功率增大到一定程度时，所产生的等离子场移动至靠近微波入口侧壁面区域，石英管内部电场强度则较低，如图4(b)(d)(f)，文献[26]研究石英管氩气等离子体放电模型时得到相类似的等离子场与微波电场对应分布。另外，其中重物质H2s的分布则同时受到介质流场的作用而相应呈现向下游运动的趋势。为寻找该现象的原因，针对这两个工况，舍去等离子体反应而只考虑微波场传输特性，得到如图5所示相应工况微波电场分布情况。
由图5(a)(b)可知，两种微波功率下，无等离子体反应时石英管内电场都符合TE模式电磁波所形成电场，即都可正常进入石英管。图5(c)对比了1000 W和1800 W两个工况有、无等离子体反应时石英管内沿中轴线（图5(a)(b)中x=0.2）电场强度分布。1800 W时，虽然无等离子体反应时在石英管内其电场明显强于1000 W时，但加入等离子体反应时其在石英管中心部分电场强度则很弱，且电场能量偏移至管内微波入口侧，且相对更强，说明该功率时微波没有有效进入石英管，并在入口处形成一定聚集效应；相比来说，1000 W时，等离子场的存在也使得进入石英管的微波电场有所减弱，但差异尚不明显。究其原因，产生的等离子体内部自由电子沿电场方向移动会产生与微波电场相反的电场，从而呈现出等离子体对于微波电场一定的阻碍[27]，保持气压一定，微波功率升高至一定临界值时，等离子体产生的反向电场变得足够强，使得微波场难以有效进入反应器石英管，相应等离子体集中于石英管上侧管壁微波入口处产生。这时壁面处表面反应R15加强使得大部分激发态H2s退激发为基态H2分子，呈现为图3中电离度保持上升，H2s浓度则先上升，而在高于一定功率后快速下降，相应H2分子浓度先下降而后快速升高的趋势。
-
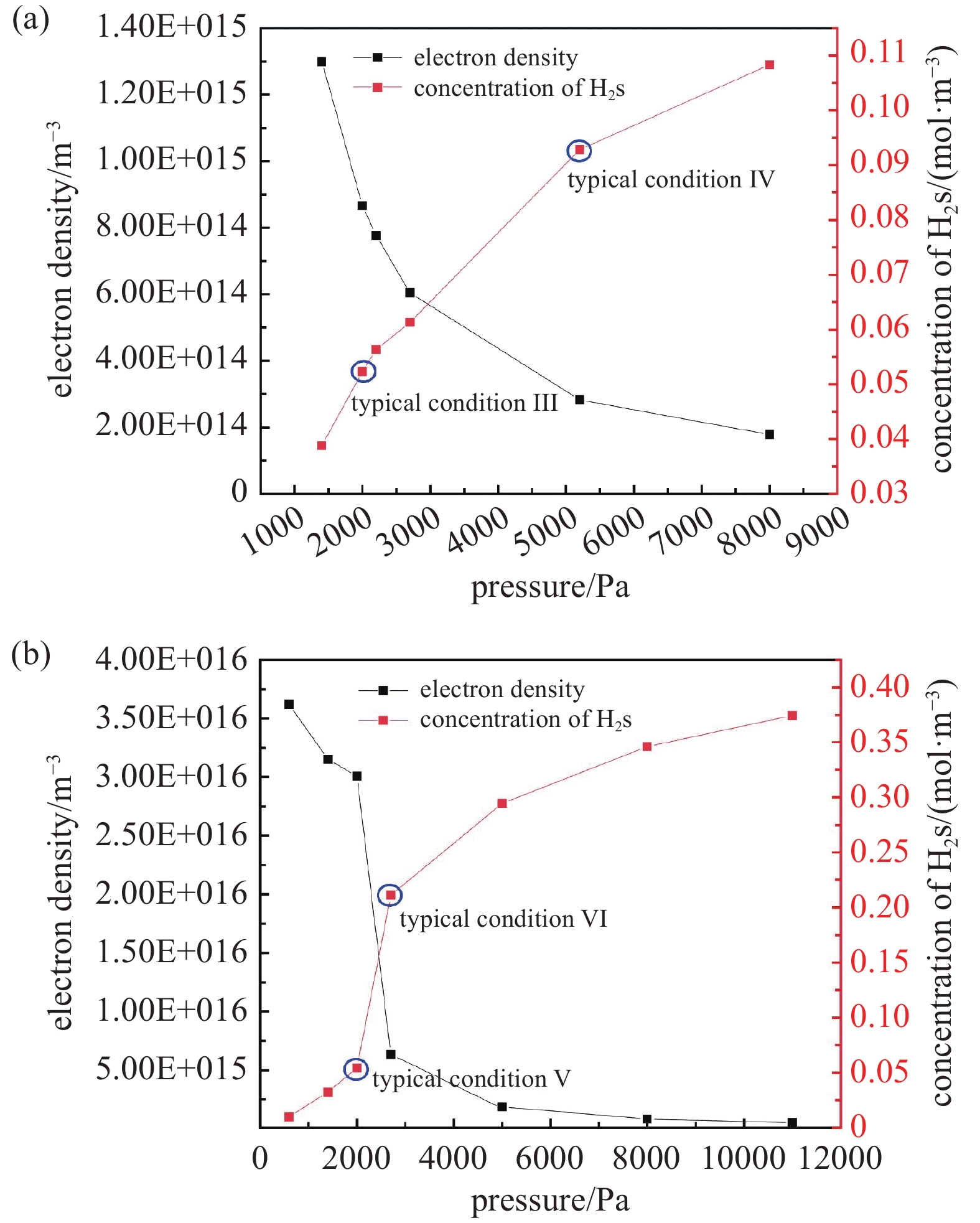
在模型温度300 K、氢气流速0.4175 m/s条件下，固定微波功率不变，设置等离子体模型压力分别为1400 Pa、2000 Pa、2700 Pa、5200 Pa和8000 Pa，其对应氢气初始浓度分别为0.56、0.80、1.08、2.08、3.21 mol/m3，取微波输入功率分别固定为600 W和2000 W对比研究，各工况管内平均电子数密度和H2s浓度变化如图6所示。
图6(a)中给出了600 W较低功率下等离子体电子密度随介质压力升高呈近似指数衰减的趋势，该现象可以从电子碰撞合理解释，在一定的输入功率下，如提高气压，会引起碰撞频率增加，但由于平均自由程减小，电子无法获得足够的能量电离介质粒子，从而导致电子密度的降低，苏小保[28]等在其探究气压对氩气放电的影响时也得到了相似的结论。另一方面，在电子碰撞达不到电离的情况下，达到激发态的分子数目相应增加，即图中H2s浓度随压力单调增加，另外，与电子密度减小趋势减缓相对应，H2s浓度增加速率也随压力增大而变小。同时，电子密度的降低，也使得H2s进一步激发至电离态的几率降低而使其而浓度上升。图6(b)中微波功率为2000 W时的等离子场结果，并相比600 W时拓展给出模型压力600 Pa和11000 Pa下的等离子体工况，使规律呈现更为清楚。可以看出，在功率较高情况下，随着压力改变，电子密度和重物质H2s依然保持与600 W相似的变化趋势，但在快速下降的临界区域下降速度更快。
为更好地揭示不同微波功率下改变压力对于等离子体放电体系的影响，选取上述两个功率下各自典型工况的等离子场进行分析，如图7所示。
由图7可知，功率较小时，等离子体场总是规则分布于石英管中央附近，而功率较大但压力较低时，则存在等离子体场聚集于管内上侧微波入口处的异常现象，其原因与上文介质压力一定而微波功率升高至一定临界值以上时类似，其电子密度较高所形成电场的反作用限制了微波的进入，使得等离子体只能在微波入口附近产生，相应H2s在壁面处大量退激发而浓度小得多，功率大同时压力也较大时，反而没有出现明显的等离子体场集聚于上部而规则分布于石英管中央的情形，说明压力大时具有与如图3、图4功率小时相类似的效果，即等离子体自身产生的反作用电场相对弱而不会阻碍微波的有效进入。从而功率大时介质气压也需要相对大才可形成正常的等离子体场，并产生高的H2s浓度。
-
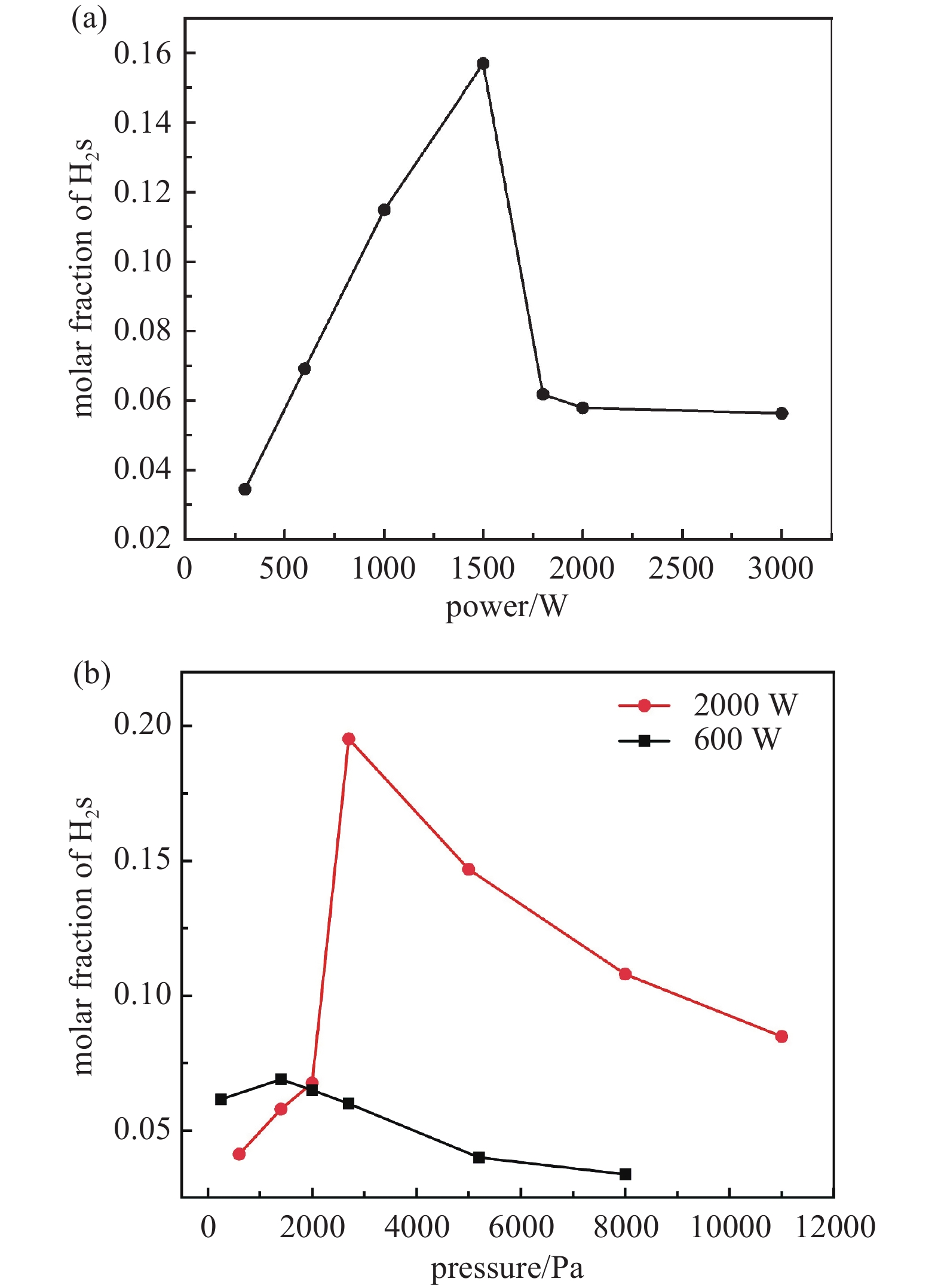
由前文研究可知，在输入功率不变的情况下，随着压力的升高，在一定范围内可以提高等离子体中H2s的摩尔浓度，但是压力升高会使得介质中所有物质的摩尔浓度都提高，所以仅采用该项指标不能完全反映等离子体的生成与变化特性，因此，进一步对比了前述不同工况下所产生等离子体中H2s摩尔分数指标，以更为全面地获得不同反应条件下产生活性物质的“效率”，更好地刻画所产生等离子体参数变化机理，结果如图8所示。
如图8(a)所示，可知压力不变的情况下，H2s摩尔分数与其摩尔浓度（对应于图3(a)）随微波功率有相同变化趋势，该现象符合固定容器中理想气体混合物状态方程所阐释规律。
分别结合图6(a)(b)，由图8(b)可知无论微波输入功率处于较高或较低水平，随着介质压力升高，都会在在某个气压会达到H2s摩尔分数的极大值，对应于电子密度快速下降结束点。以微波功率2000 W为例，随着压力升高，H2s的摩尔分数会先升高，在2700 Pa到达峰值后又快速下降，说明在相应功率下2700 Pa时氢气分子产生激发态的“效率”最高。当微波功率为600 W时，达到H2s摩尔分数峰值的气压小于2000 W下峰值的气压，为~1400 Pa。另外，压力较低时，功率2000 W时的H2s摩尔分数相比600 W时偏低，而在压力较高时，则比后者值大得多。
总的来说，不同参数变化，H2s转化效率均存在一峰值。以2000 W时随压力的变化规律为例，结合图6(b)、图7及图8(b)，随着压力降低（即逆横轴方向），H2s的浓度相对降低，而H2s摩尔分数则相对升高，2700 Pa时转化效率在各工况中达最大，即图8(b)中相应峰值位置，进一步降低气压，到2000 Pa时由于如前述原因，即等离子场自身产生的反作用电场增大至阻止了微波电场的有效进入，使得等离子体聚集于上侧壁面使H2s大量退激发，从而表现为H2s转化效率降低。其它参数变化过程为类似规律，即不同参数变化过程均存在一最佳（也是极限）的气压与微波功率的匹配，其H2s转化效率相应最大，超过相应临界值进一步增大功率或减小气压，均会因等离子体反作用电场增大至阻碍微波有效进入造成H2s转化效率相应降低。
-
微波氢等离子体还原氧化铁具有明显优点与前景，但其机理尚不明确，鉴于此本文建立了微波谐振腔等离子体放电模型，在已有文献实验结果对模型有效验证基础上，开展数值理论研究并得到了等离子体特征参数随微波工况变化的相关规律。主要结论如下：
(1) 介质压力一定时，微波功率输入的提高有利于气体放电效率的提高，所产生等离子体中的电子密度单调升高；而H2s的浓度随微波功率的变化则存在一极大值，相应存在一临界微波功率，超过该临界值时，所产生的等离子场对微波电场形成的反作用将使微波难以有效进入反应器，并使得等离子体反应聚集于微波进入反应器的入口处，而该处在壁面上表面反应的相应加剧使得大量H2s退激发为H2。
(2) 在一定微波入射功率下，气体压力升高时，由于电子平均自由程变小而限制电离反应的发生，使得氢气等离子体体系的电子密度下降，相应地获得了更高浓度的H2s。压力高于一临界值时，电子密度减小至所形成反作用电场不再能够阻止微波的有效进入，反应更分散，电子密度快速减小至一定值后趋势变缓，H2s浓度也在快速增大至一定值后增速趋缓。
(3) 与压力一定改变微波功率的等离子体场变化规律不同，大功率条件下，压力较低时所产生的较高等离子体电子密度同样阻碍微波入射，并使得所产生等离子体场聚集于石英管上侧壁面微波入口处，大量H2s退激发为H2，而随着压力升高而超过相应临界值，所产生等离子体场则可规则分布于石英管中央。
(4) 固定微波功率升高气压时虽可以提高H2s的摩尔浓度，但其摩尔分数则存在峰值；固定压力升高功率时，H2s的摩尔分数和摩尔浓度有一致的趋势。
总体上，微波输入功率和等离子体介质压力需要合适的匹配，压力较低时，需要较低的微波功率，微波功率较高时，需要较高的介质压力，以获得合理的等离子体反应场及尽可能高的H2转化为活性物质的效率。
微波氢等离子体反应特性研究
Reaction Characteristics of Microwave Hydrogen Plasma
-
摘要: 氢气作为未来主要的清洁能源，将在未来绿色冶金领域发挥关键作用。本文以低温等离子体辅助氢气直接还原炼铁为背景，基于不同已有等离子体反应模型和LXcat数据库建立了二维微波氢气等离子体模型。对比文献实验结果验证了所建立等离子体反应模型和体系的正确与合理性，在此基础上研究得到了微波功率和气体压力变化对等离子体电子密度、以及在铁矿石还原中起主要作用的激发态氢气分子浓度等关键参数的影响特性。结果表明，介质压力一定而微波功率升高，则电子密度升高，但激发态氢气摩尔浓度存在一明显峰值变化过程；当微波功率一定而介质压力升高，则电子密度呈一定指数下降趋势，激发态氢气摩尔浓度保持单调递增状态，不过激发态氢气摩尔分数变化则存在一峰值。另外，分析讨论了微波功率相对过大或气体压力相对过小氢气分子激发态浓度及摩尔分数出现峰值变化的原因与特性。本研究在一定程度上揭示了微波等离子体随微波参数变化的机理特征，可为氢气还原氧化铁绿色冶金相关理论进一步研究和应用提供参考。Abstract: Hydrogen will be the main clean energy in the future, which will play a key role in the future’s green metallurgy. Taking low temperature plasma aided hydrogen direct reduction rection of iron ore as a background, a two-dimensional numerical model was established to study the reaction characteristics of microwave hydrogen plasma by combining reaction mechanisms from different literature and data from LXcat database. Compared with the experimental results in the literature, the rationality and reliability of the plasma model were verified. Based on that, the effects of the input power of the microwave and gas pressure of the plasma on the indicators such as electron density and concentration of excited hydrogen molecule (H2s) in the plasma were investigated, which obtained key parameters for the iron ore reduction. The results show that, at a constant pressure of plasma medium and an increasing input power of the microwave, the electron density increases, while there exists a peak value with the H2s concentration. When the pressure of the plasma medium increases, at a certain microwave power, the electron density decreases exponentially, and the H2s concentration keeps monotonically increasing, whereas its molar fraction shows a peak with the variation. Furthermore, the reasons and characteristics for having peak in variation of the concentration and the fraction of H2s, respectively, in the plasma reaction are discussed when the microwave power or the gas pressure reaches beyond a critical value. Such a study is expected to provide a theoretical reference for further research and application of hydrogen plasma iron oxide reduction in green iron making.
-
Key words:
- Low temperature plasma /
- Microwave /
- Electron density /
- Excitation hydrogen molecule /
- Green iron-making .
-
-
图 1 石英管谐振腔模型，(a) 几何模型, (b) 网格划分, (c) 网格无关性验证
Figure 1. Geometric model of the quartz tube resonator (a), mesh (b), and grid independence verification (c)
图 3 微波功率对各物质场平均浓度影响: (a) 电子密度及H2s浓度 (b) 其它重物质粒子浓度
Figure 3. Effect of microwave power on (a) electron density, concentration of H2s and (b) concentration of H, H2, H2+, H+, Hs
图 5 图3中两典型工况对应于无等离子体反应时的微波电场分布(V/m): (a) 1000 W, (b) 1800 W. (c)有、无等离子体反应时电场沿竖中轴线分布对比
Figure 5. Electric field (V/m) distribution at 1000 W (a) and 1800 W (b) without plasma reaction; and comparison between the conditions with/without plasma at the two powers, along the erect central axis (c)
图 6 600 W (a)和2000 W (b)时场平均电子密度、H2s浓度随压力变化趋势
Figure 6. Trend diagram of field averaged electron density and H2s concentration with pressure under 600 W (a) and 2000 W (b)
图 7 不同微波功率和介质压力典型工况下等离子体电子密度分布。 600 W时: (a) 2000 Pa, (b) 5200 Pa; 以及2000 W时: (c) 2000 Pa; (d) 2700 Pa
Figure 7. Diagram of electron density (m−3) distribution at different microwave power and medium pressure, respectively
图 8 H2s摩尔分数: (a) 1400 Pa压力下随微波功率的变化; 及(b)功率一定随气压的变化
Figure 8. Change of H2s molar fraction with: (a) microwave power at 1400 Pa; (b) pressure at a constant microwave power
No. Reaction equation Reaction type Rate coefficient /m3∙(s∙mol)-1 R1 e+H2=>e+H2 Elastic collision Collision cross section R2 e+H2=>e+2H Dissociation Collision cross section R3 e+H2=>2e+H2+ Ionization Collision cross section R4 e+H2=>e+H2s Excitation Collision cross section R5 e+H=>e+Hs Excitation Collision cross section R6 e+H=>2e+H+ Ionization Collision cross section R7 e+H2+=>e+H++H Excitation 6.9268E-14 R8 e+H2s=>H2++2e Ionization 3.99E-10 R9 e+H3+=>H2+H Attachment 1.33E-8 
下载: 导出CSV
No. Reaction equation Reaction type Rate coefficient/m3∙(s∙mol)−1 R10 H2+H2=>H+H+H2 Somatic reaction 8.13E-17 R11 H2+H2+=>H3++H Somatic reaction 1.99E-9 R12 H3+=>H+H2 Surface reaction Based on adhesion coefficient R13 H+=>H Surface reaction Based on adhesion coefficient R14 H2+=>H2 Surface reaction Based on adhesion coefficient R15 H2s=>H2 Surface reaction Based on adhesion coefficient R16 Hs=>H Surface reaction Based on adhesion coefficient
下载: 导出CSV
-
[1] Sabat K C,Rajput P,Paramguru R K,et al. Reduction of oxide minerals by hydrogen plasma: an overview[J]. Plasma Chemistry & Plasma Processing,2014,34(1):1−23 [2] Sabat K C. Physics and chemistry of solid state direct reduction of iron ore by hydrogen plasma[J]. Фізика і хімія твердого тіла,2021,22(2):292−300 [3] 贺新福. 甲烷低温等离子体活化与煤热解耦合过程研究[D]. 大连: 大连理工大学, 2012 He X F. Integrated Process of Coal Pyrolysis with Methane Activation by Cold Plasma[D]. Dalian: Dalian University of Technology, 2012 [4] Guan Y X. Microwave Plasma Technology and Research Progress[J]. Safety Health & Environment,2020,20(2):1−5 (关银霞. 微波等离子体技术及研究进展[J]. 安全, 健康和环境,2020,20(2):1−5(in chinese) Guan Y X. Microwave Plasma Technology and Research Progress[J]. Safety Health & Environment, 2020, 20(2): 1-5( [5] Hrebtov M Y,Bobrov M S. Numerical optimization of hydrogen microwave plasma reactor for diamond film deposition[J]. Journal of Physics:Conference Series,2019,1382:012010 doi: 10.1088/1742-6596/1382/1/012010 [6] Wang F Y,Meng X M,Tang W Z,et al. Simulation of Hydrogen and Argon Microwave Plasma in a Cylindrical Microwave Plasma Chemical Vapor Deposition Reactor[J]. Vacuum and Cryogenics,2008(03):157−163 (王凤英,孟宪明,唐伟忠,等. 圆柱谐振腔式MPCVD装置中氢、氩微波等离子体分布规律的数值模拟[J]. 真空与低温,2008(03):157−163(in chinese) Wang F Y, Meng X M, Tang W Z, et al. Simulation of Hydrogen and Argon Microwave Plasma in a Cylindrical Microwave Plasma Chemical Vapor Deposition Reactor[J]. Vacuum and Cryogenics, 2008(03): 157-163( [7] 谷昊周. 微波等离子体化学气相沉积谐振腔的数值仿真与研究[D]. 杭州: 杭州电子科技大学, 2022 Gu H Z.Numerical simulation and stuy of resonant cavities for microwave plasma chemical vapour deposition[D]. Hangzhou: Hangzhou Dianzi University, 2022 [8] Zhu H F,Wang Y K,Ding W M,et al. Preparation of diamond films by low power MPCVD[J]. Diamond & Abrasives Engineering,2021,41(02):39−45 (朱海丰,王艳坤,丁文明等. 低功率MPCVD制备金刚石薄膜[J]. 金刚石与磨料磨具工程,2021,41(02):39−45(in chinese) doi: 10.13394/j.cnki.jgszz.2021.2.0007 Zhu H F, Wang Y K, Ding W M, et al. Preparation of diamond films by low power MPCVD[J]. Diamond & Abrasives Engineering, 2021, 41(02): 39-45 doi: 10.13394/j.cnki.jgszz.2021.2.0007 [9] Wang B,Wang J H,Weng J,et al. Effect of Gas Flow Mode on Uniformity of MPCVD Diamond Films[J]. Vacuum and Cryogenics,2020,26(02):108−113 (王斌,汪建华,翁 俊等. 气体流动方式对MPCVD金刚石薄膜均匀性的影响[J]. 真空与低温,2020,26(02):108−113(in chinese) doi: 10.3969/j.issn.1006-7086.2020.02.004 Wang B, Wang J H, Weng J, et al. Effect of Gas Flow Mode on Uniformity of MPCVD Diamond Films[J]. Vacuum and Cryogenics, 2020, 26(02): 108-113( doi: 10.3969/j.issn.1006-7086.2020.02.004 [10] Hao J M,Zhu J,Chen Y N,et al. Reduction of Fe2O3 by Atmospheric Pressure Cold Plasma Jet[J]. Surface Technology,2017,46(03):151−156 (郝建民,朱 军,陈永楠,等. 常压低温冷等离子体还原Fe2O3的研究[J]. 表面技术,2017,46(03):151−156(in chinese) Hao J M, Zhu J, Chen Y N, et al.Reduction of Fe2O3 by Atmospheric Pressure Cold Plasma Jet[J]. Surface Technology, 2017, 46(03):151-1556( [11] Zhang Y W,Ding W Z,Guo S Q,et al. Reduction of Metal Oxide by Non-equlibrium Hydrogen Plasma[J]. Shanghai Metals,2004(04):17−20 (张玉文,丁伟中,郭曙强,等. 非平衡等离子态氢还原金属氧化物的实验[J]. 上海金属,2004(04):17−20(in chinese) doi: 10.3969/j.issn.1001-7208.2004.04.005 Zhang Y W, Ding W Z, Guo S Q, et al. Reduction of Metal Oxide by Non-equlibrium Hydrogen Plasma[J]. Shanghai Metals, 2004(04): 17-20( doi: 10.3969/j.issn.1001-7208.2004.04.005 [12] 郭曙强, 丁伟中, 张玉文. 氧化铁球团在低温氢等离子体中的还原[C]//2002全国冶金物理化学学术会议, 中国金属学会, 2002: 504-507 Guo S Q, Ding W Z, Zhang Y W. Reduction of Fe2O3 Pellet in Non-equlibrium Hydrogen Plasma[C]//2002 National Symposium on Metallurgical Physics and Chemistry, CSM, 2002:504-507 [13] Sabat K C,Murphy A B. Hydrogen plasma processing of iron ore[J]. Metallurgical & Materials Transactions B,2017,48(3):1561−1594 [14] Rajput P,Sabat K C,Paramguru R K,et al. Direct reduction of iron in low temperature hydrogen plasma[J]. Ironmaking & Steelmaking,2014,40(10):61−68 [15] Xu M,Zhang W B. Research on Process of Reduction of Ilmenite by Microwave Plasma[J]. Vacuum and Cryogenics,2011,17(04):209−212+223 (徐慢,张文波. 微波等离子体还原钛铁矿工艺研究[J]. 真空与低温,2011,17(04):209−212+223(in chinese) doi: 10.3969/j.issn.1006-7086.2011.04.005 Xu M, Zhang W B. Research on Process of Reduction of Ilmenite by Microwave Plasma[J]. Vacuum and Cryogenics, 2011, 17(04): 209-212+223( doi: 10.3969/j.issn.1006-7086.2011.04.005 [16] Wei B,Guo H X,Ding S S,et al. Design an Simulation of Microwave Plasma Reactor[J]. Safety & EMC,2020(04):87−92 (卫博,郭海霞,丁叁叁等. 微波等离子体反应器的设计与仿真[J]. 安全与电磁兼容,2020(04):87−92(in chinese) Wei B, Guo H X, Ding S S, et al. Design an Simulation of Microwave Plasma Reactor[J]. Safety & EMC, 2020(04): 87-92( [17] Mankelevich Y A,Ashfold M,Ma J. Plasma-chemical processes in microwave plasma-enhanced chemical vapor deposition reactors operating with C/H/Ar gas mixtures[J]. Journal of Applied Physics,2008,104(11):473 [18] Rajput P,Bhoi B,Sahoo S,et al. Preliminary investigation into direct reduction of iron in low temperature hydrogen plasma[J]. Ironmaking & Steelmaking,2013,40(1):61−68 [19] Janev R K, Langer W D, Evans K, et al. Elementary processes in hydrogen-helium plasmas: Cross sections and reaction rate coefficients[M]. Elementary Processes in Hydrogen-Helium Plasmas, 1987. [20] Kimura T,Kasugai H. Properties of inductively coupled radio frequency CH4/H2 Plasmas: experiments and global model[J]. Japanese Journal of Applied Physics,2012,51(4):6202 [21] Hassouni K,Grotjohn T A. Self-consistent microwave field and plasma discharge simulations for a moderate pressure hydrogen discharge reactor[J]. Journal of Applied Physics,1999,86(1):134−151 doi: 10.1063/1.370710 [22] 李唤. 微波等离子体及其功能薄膜沉积[D]. 合肥: 中国科学技术大学, 2017 Li H. Microwave Plasma and Deposition of Functional Films[D]. Hefei: University of Science and Technology of China, 2017 [23] Bouherine K,Tibouche A,Ikhlef N,et al. 3-D numerical characterization of a microwave argon PECVD plasma reactor at low pressure[J]. IEEE Transactions on Plasma Science,2016,44:3409−3416 doi: 10.1109/TPS.2016.2619696 [24] 王超. 甲烷针—板放电等离子体的数值模拟及特性研究[D]. 济南: 山东师范大学, 2018 Wang C. Numerical simulation and characterization of methane needle-plate discharge plasma[D]. Jinan: Shandong Normal University, 2018 [25] Hassouni K,Gicquel A,Capitelli M,et al. Chemical kinetics and energy transfer in moderate pressure H2 plasmas used in diamond MPACVD processes[J]. Plasma Sources Science and Technology,1999,8(3):494 doi: 10.1088/0963-0252/8/3/320 [26] Shen Q,Huang R,Xu Z,et al. Numerical 3D modeling: microwave plasma torch at intermediate pressure[J]. Applied Sciences,2020,10(15):5393 doi: 10.3390/app10155393 [27] 张晓友, 戚东升, 何锋, 等. 等离子体对电磁波的阻挡作用研究[C]//中国物理学会第十三届静电学术年会, 中国物理学会, 2006: 193-196 Zhang X Y, Qi D S, He F, et al. Study on Block of Electromagnetic Wave by Plasma[C]//The 13th Annual Electrostatic Conference of the Chinese Physical Society, CPS, 2006: 193-196 [28] Su X B,Wu Q C,Wan Y X. The Effect of Pressure on the Argon Plasma Characterization[J]. Vacuum and Cryogenics,1997,3(4):3−7 (苏小保,邬钦崇,万元熙. 气压对氩等离子体特性的影响[J]. 真空与低温,1997,3(4):3−7(in chinese) Su X B, Wu Q C, Wan Y X. The Effect of Pressure on the Argon Plasma Characterization[J]. Vacuum and Cryogenics, 1997, 3(4): 3-7( -
图( 8) 表( 2)
计量
- 文章访问数: 108
- HTML全文浏览数: 108
- PDF下载数: 2
- 施引文献: 0